Post-apocalyptic programming
We got deadly viruses, nuclear war threats, economy heading from one crisis to another deeper crisis, politicians going out of control… You know that feeling. The end is near, isn’t it?
But let’s talk about brighter things – technology. We are all smart people, working on valuable and complex software projects in great agile teams, copying code from Stack Overflow and using GitHub co-pilot to help us with the routine.
Now, what if you are the only survivor with some programming skills sitting in front of a computer you’ve never heard of, with some hex pad to enter machine codes, with maybe some pen and paper. What will you do?
In this not-so-short article we will try to go a full cycle from exploring the CPU, building an assembler, building the core of the Forth VM and finally building a reasonably useful Forth interpreter. Beware, this might contain unwanted low-level details as well as some meta-programming parts.
If code speaks better to you then words - you may find the emulator, the assembler, the VM and the Forth code sample at github.com/zserge/lc3-forth. It’s only 0.5KB of machine code, or ~400 lines of C.
The CPU
If we managed to get a chip crisis in a peaceful modern era – then in a post-apocalyptic world I wouldn’t rely on a good supply for x86 or ARM64 chips. Not to mention those would be very hard to program by hand. Instead I would imagine some low-end microcontrollers with a dozen of supported primitive instructions. Something even a hobbyist could build in Verilog.
To keep things fun let’s start with something simple and familiar, probably the CPU you’ve learned during your CS classes. I’m talking about the good old LC-3. It’s known to be a good educational model, and the instruction set is super tiny and convenient to be entered by hand in hexadecimal form:
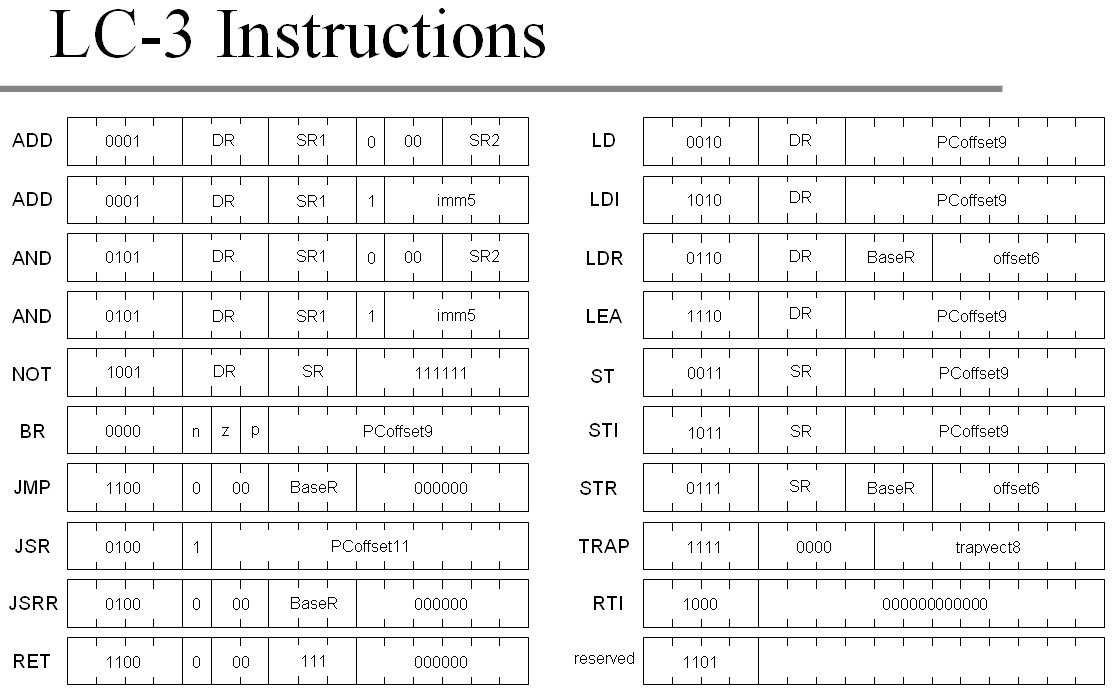
There are 15 instructions that we care about: ADD, AND, NOT are the only arithmetic operations we got, BR, JMP, JSR and RET are the only branching instructions, LD, LDI, LDR with ST STI, STR counterparts are all load/store instructions, LEA helps with indirect addressing and TRAP handles the I/O.
It’s a 16-bit CPU that is even incapable of loading an 8-bit immediate value into its registers. It got 8 registers in total, of which the last one is used as a return address pointer for subroutines, so should be used with care. The rest are pretty orthogonal.
To simulate our apocalypse let’s start with an emulator for this toy CPU, it shouldn’t be too hard.
LC-3 Simulator
I will be using C to keep the grim atmosphere of the apocalypse, but you may try this exercise in a different language, of course.
We know that LC-3 stores code and data together, has 8 registers and the instruction cycle works as follows: it fetches the next instruction from memory increasing the program counter, it decodes the fetched instruction, it evaluates the relative addresses if needed, loads operands such as registers or immediate values, executes the operation and stores the result in a register or in memory.
Our emulator would be a function that performs one instruction cycle. Calling that function in a loop would execute the LC-3 program.
Two things to consider prior to that is how LC-3 handles negative numbers and how it handles the braching flags. LC-3 has a concept of “sign extension” - an operation of increasing the number of bits in an integer while preserving the sign and the value. You may have noticed that some instructions use lower bits for immediate values - it may be 6 lowest bits, or 9 lowest bits. At the end these become 16-bit numbers, because the CPU deals only with 16-bit values. The CPU extends such operands into 16-bit numbers keeping their sign. In C we can implement it like this:
static int sext(int x, int bits) {
int m = (1 << (bits - 1));
int n = x & ((1 << bits) - 1);
return (n ^ m) - m;
}
sext(0x15, 5); // => 10101 becomes 11111111 11110101 = 0xfff5 = -11
sext(0x05, 5); // => 00101 becomes 00000000 00000101 = 0x0005 = 5
When it comes to branching, LC-3 supports 3 conditional flags stored in a special non-addressable register, these flags are updated after all arithmetic and load instructions. They are Z (result is zero), P (result is positive) or N (result is negative). Only one flag can be set at a time. We could have a convenience function for them:
static int flags(int x) {
return (x < 0) * 4 + (x == 0) * 2 + (x > 0);
}
We are ready to write our LC-3 instruction handler:
#define OP(_hint, code, body) case code: body; return pc;
#define CC(x) reg[8] = flags(x)
static int lc3(int *mem, int *reg, int pc) {
int op = mem[pc];
int x = (op >> 9) & 7;
int y = (op >> 6) & 7;
int z = (op & 0x3f);
pc++;
switch (op >> 12) {
OP(BR, 0, pc += (reg[8] & x) ? sext(op, 9) : 0)
OP(ADD, 1, CC(reg[x] = reg[y] + ((z & 0x20) ? sext(op, 5) : reg[z])))
OP(LD, 2, CC(reg[x] = mem[pc + sext(op, 9)]))
OP(ST, 3, mem[pc + sext(op, 9)] = reg[x]);
OP(JSR, 4, (reg[7] = pc, pc = pc + sext(op, 9)))
OP(AND, 5, CC(reg[x] = reg[y] & ((z & 0x20) ? sext(op, 5) : reg[z])));
OP(LDR, 6, CC(reg[x] = mem[reg[y] + sext(op, 6)]));
OP(STR, 7, mem[reg[y] + sext(op, 6)] = reg[x]);
OP(NOT, 9, CC(reg[x] = ~reg[y]));
OP(LDI, 10, CC(reg[x] = mem[mem[pc + sext(op, 9)]]));
OP(STI, 11, mem[mem[pc + sext(op, 9)]] = reg[x]);
OP(JMP, 12, pc = reg[y]);
OP(LEA, 14, CC(reg[x] = pc + sext(op, 9)));
OP(TRAP,15, (z == 0x20) ? reg[0] = getchar() : (z == 0x21) ? putchar(reg[0]) : (pc = (z == 0x25 ? -1 : pc)));
}
return -1;
}
We start with fetching the instruction (op = mem[pc]), then decoding it into x/y/z parts, where X is usually a destination register, Y is the source register and Z is the immediate part. Not all instructions use them like that, but most do. We increase the PC as part of the fetch phase, and check the top 4 bits of the opcode.
The OP macro defines an operation, mnemonics for better clarity, and the body of the operation as a single C statement, typically reg[x] = ... or mem[..] = .... At the end OP returns the PC, which might be modified by the operation.
CC macro set the flag register depending on the value of the result, and returns the result. Branching, store and trap instructions don’t change CC flags, but other operations do.
AND and ADD instructions check for the 0x20 (bit 6) to decide if the operant is an immediate value or a register. TRAP is the longest operation. It handles 0x20 trap to read a byte from console, 0x21 trap to print a byte and 0x25 to terminate the execution. When pc becomes negative - the emulator should stop.
Running LC-3 programs with this emulator is as simple as:
int asmbuf[0xffff] = { ... LC-3 program ... };
int pc = 0x3000;
int reg[9] = {0};
while (pc) {
pc = lc3(asmbuf, reg, pc);
}
Even though it’s possible to write LC-3 programs by hand using hexadecimal machine codes, we have a tough road ahead, so let’s build a small assembler.
LC-3 Assembler
Since we started with C, I would reuse the language for assembly as well. Instead of writing a CLI tool that parses assembler syntax and generates machine code, I’d rather create some helper C functions that would fill asmbuf with machine codes. In this case we would be able to assemble and run machine code from the same C program.
Let’s introduce asmptr pointer to asmbuf, that would be advanced with every assembly instruction compiled:
static int asmbuf[0xffff];
static int *asmptr = asmbuf + 0x3000;
...
static void RET() { *asmptr++ = 0xc1c0; }
static void TRAP(int op) { *asmptr++ = 0xf000 | (op & 0xff); }
...
What about instructions that take register operands? We would need an enum of all available registers R0..R7. But how do we tell a register from an immediate value? We could introduce special functions ADDI and ANDI to deal with immediate values, but we might not need that. We only need to represent registers 0..7 and immediate numbers in the range -15..15. So we can use a special mask, say top 4 bits to be set to 1010 for register and 1111/0000 for negative or positive immediates:
#define _R(n) ((n & 7) | 0xa000) /* helper to define register enum */
#define NR(r) (r & 7) /* register number 0..7 */
#define DR(r) (NR(r) << 9) /* destination register operand */
#define SR(r) (NR(r) << 6) /* source register operand */
#define IR(x) (((x >> 12) == 0xa) ? NR(x) : ((x & 0x1f) | 0x20)) /* imm or reg */
#define A9(a) ((a) & 0x1ff) /* PCOffset9 nine-bit arg */
enum {R0 = _R(0), R1 = _R(1), R2 = _R(2), R3 = _R(3), R4 = _R(4), R5 = _R(5), R6 = _R(6), R7 = _R(7)};
What’s left is jumps and addresses. In a normal assembler there are labels where code can jump to. We would have to use C variables for labels. It would be more convenient for assembler “instructions” to return current address where the instruction is stored. The we could write assembly like this:
int label;
label = ADD(R0, R0, 1);
BR(label);
Since we have asmptr pointer - the offset between that and asmbuf is the address. We can define a helper that returns that difference and use that in all instructions. After all these tweaks we finally have all instructions ready:
static int asmbuf[0xffff], *asmptr = asmbuf + 0x3000, asmrun = 0;
#define _R(n) ((n & 7) | 0xa000) /* helper to define register enum */
#define NR(r) (r & 7) /* register number 0..7 */
#define DR(r) (NR(r) << 9) /* destination register arg */
#define SR(r) (NR(r) << 6) /* source register arg */
#define IR(x) (((x >> 12) == 0xa) ? NR(x) : ((x & 0x1f) | 0x20)) /* imm or reg */
#define A9(a) ((a) & 0x1ff) /* PCOffset9 arg */
enum {R0 = _R(0), R1 = _R(1), R2 = _R(2), R3 = _R(3), R4 = _R(4), R5 = _R(5), R6 = _R(6), R7 = _R(7)};
#define _L(x) { x; return asmptr - asmbuf - 1; }
static int PC() { return asmptr - asmbuf; }
static int DW(int n) { *asmptr++ = n; return PC() - 1; }
static int LL(int label) { return label - PC() - 1; }
static int BR(int addr) { _L(*asmptr++ = 0x0e00 | A9(LL(addr))); }
static int BRN(int addr) { _L(*asmptr++ = 0x0800 | A9(LL(addr))); }
static int BRZ(int addr) { _L(*asmptr++ = 0x0400 | A9(LL(addr))); }
static int BRP(int addr) { _L(*asmptr++ = 0x0200 | A9(LL(addr))); }
static int BRNZ(int addr) { _L(*asmptr++ = 0x0c00 | A9(LL(addr))); }
static int BRNP(int addr) { _L(*asmptr++ = 0x0a00 | A9(LL(addr))); }
static int BRZP(int addr) { _L(*asmptr++ = 0x0600 | A9(LL(addr))); }
static int ADD(int x, int y, int z) { _L(*asmptr++ = 0x1000 | DR(x) | SR(y) | IR(z)); }
static int AND(int x, int y, int z) { _L(*asmptr++ = 0x5000 | DR(x) | SR(y) | IR(z)); }
static int NOT(int x, int y) { _L(*asmptr++ = 0x9000 | DR(x) | SR(y) | 0x3f); }
static int LEA(int x, int addr) { _L(*asmptr++ = 0xe000 | DR(x) | A9(LL(addr))); }
static int LD(int x, int addr) { _L(*asmptr++ = 0x2000 | DR(x) | A9(LL(addr))); }
static int LDI(int x, int addr) { _L(*asmptr++ = 0xa000 | DR(x) | A9(LL(addr))); }
static int ST(int x, int addr) { _L(*asmptr++ = 0x3000 | DR(x) | A9(LL(addr))); }
static int STI(int x, int addr) { _L(*asmptr++ = 0xb000 | DR(x) | A9(LL(addr))); }
static int LDR(int x, int y, int z) { _L(*asmptr++ = 0x6000 | DR(x) | SR(y) | (z & 0x3f)); }
static int STR(int x, int y, int z) { _L(*asmptr++ = 0x7000 | DR(x) | SR(y) | (z & 0x3f)); }
static int JMP(int x) { _L(*asmptr++ = 0xc000 | SR(x)); }
static int JSR(int addr) { _L(*asmptr++ = 0x4800 | A9(LL(addr))); }
static int RET() { _L(*asmptr++ = 0xc000 | SR(R7)); }
static int TRAP(int op) { _L(*asmptr++ = 0xf000 | (op & 0xff)); }
static int GETC() { _L(TRAP(0x20)); }
static int PUTC() { _L(TRAP(0x21)); }
static int HALT() { _L(TRAP(0x25)); }
#define LC3ASM() for (asmrun=2; asmrun && (asmptr = asmbuf + 0x3000); asmrun--)
LL is used for label addressing, since LC-3 uses relative jumps - instructions should contain offsets and not immediate addresses. LC3ASM is a helper macro to run assembly twice. The reason for a two-pass assembler is to handle labels that go after they are used, i.e.:
int label;
LC3ASM {
BR(label);
...
label = AND(R0, R0, 0);
...
}
On the first run label is an invalid address, which only becomes known when the first run is complete. On the second run asmbuf is regenerated with the correct address.
We can now write some assembly code and run it in the emulator. We can instrument our debugger to print register values, certain addresses, everything that we need as we will be building a more high-level language for our hand-crafted CPU.
A few notes on LC-3 assembly. There are no mov instructions. We would have to use arithmetics instead. There is also no subtraction, it should be done manually with negation and addition:
// To mov 5 into R0
AND(R0, R0, 0); // R0 := 0
ADD(R0, R0, 5); // R0 := R0 + 5
// To subtract R2 from R3:
NOT(R2, R2); // R2 := ~R2;
ADD(R2, R2, 1); // R2 := ~R2 + 1 (AKA -R2);
ADD(R3, R3, R2); // R3 := R3 + (~R2 + 1) = R3 - R2
These constructs will happen often in our further assembly code. Perhaps I should have made macro-instructions for them.
Line input
The language we are going to implement using our LC-3 assembler is a Forth dialect, inspired by SectorForth. Before going deep into the language details we should figure out how to get user input. Forth uses space-separated words as the only language syntax, so naturally all input is line-oriented. First a line is stored into the so-called “terminal input buffer” (TIB), then it’s split into words and consumed word by word.
Our first task would be to read a line from the console into TIB. We would have to define the start address of the TIB. Then we would need a loop calling TRAP(0x20) to read a byte from console into R0 and store it inside TIB, advancing the pointer. The loop should continue until a newline is found. Ideally, we should check for buffer overflow, but it’s end of the world as we know it, so we can afford making some bugs.
const int TIB = 0x4000; /* start of the terminal input buffer */
const int TOIN = 0x4100; /* next char in TIB (>IN) */
/* readln: read a line until CR and fill in the TIB */
readln = LD(R1, tib); /* load TIB address */
LD(R0, toin); /* load >IN address */
STR(R1, R0, 0); /* make >IN point at the start of TIB */
readlp = TRAP(0x20); /* r0 = getchar() */
STR(R0, R1, 0); /* mem[r1] = r0 */
ADD(R1, R1, 1); /* r1 = r1 + 1 */
ADD(R0, R0, -10); /* is r0 == '\n' ? */
BRNP(readlp); /* no: read another character */
ADD(R1, R1, -1); /* r1 = r1 - 1 to erase newline */
STR(R0, R1, 0); /* write 0 instead */
TRAP(0x25); /* halt */
toin = DW(TOIN);
tib = DW(TIB);
Since the addresses for TIB and >IN are rather large integers - we can’t load them directly, so we use intermediate cells containing the addresses and load them using LD. The rest is hopefully clear from the comments. >IN is not used in this read loop, but it’s reset at the beginning so that the parser would continue fetching words from the beginning of the buffer after the line is read.
You can try running this code in our simulator. It would read a line and terminate. Printing out the contents of asmbuf[0x4000...] would show the entered line with a zero terminator at the end.
This code chunk uses R0 and R1 but the results are not passed via registers, rather via variables. For all the following code we would consider R0..R3 as “dirty” working registers, their initial values might be random, but functions can use them any time up to their needs. Registers R4..R7 would be special, they would have their own meaning in Forth, but we’ll cover it later. So let’s be lean when choosing which register to use.
Parser
Now once we have a line read into TIB, we can start parsing it word by word. We would need a few loops here. First we need to skip leading whitespace. This would be the start of the word. Then we need to iterate over all non-whitespace bytes until the null terminator or a whitespace is found. That would be the end of the word.
Additionally, we would have to call the previous readln routine if the buffer is empty to read more data. Slightly adjusting readln we can build a token subroutine that always returns R2 pointing at the beginning of the next word token and R3 containing the length of that word:
/* token: parse a word from TIB, return its address (R2) and length (R3) */
token = LDI(R3, toin); /* r2 := >IN */
LD(R1, space); /* r1 := ' ' (0x20) (ADD can't use imm 0x20, too big) */
skipws = LDR(R0, R3, 0); /* r0 := mem[>IN] */
BRZ(readln); /* (r0 == '\0') ? read another TIB */
AND(R2, R3, R3); /* r2 := r3 (r2 is start of the token) */
ADD(R3, R3, 1); /* r3 := r3 + 1, next char */
ADD(R0, R0, R1); /* (r0 == ' ') ? skip whitespace */
BRZ(skipws);
ADD(R3, R3, -1); /* r3 := r3 - 1, roll back one char for the next loop */
findws = ADD(R3, R3, 1); /* r3 := r3 + 1, go to next char */
LDR(R0, R3, 0); /* r0 := mem[r3] */
BRZ(tokend); /* (r0 == '\0') ? done */
ADD(R0, R0, R1); /* (r0 <> ' ') ? not a space, continue */
BRNP(findws);
tokend = STI(R3, toin); /* >IN := r3 */
NOT(R1, R2); /* r1 := ~r2 */
ADD(R1, R1, 1); /* r1 := ~r2 + 1 */
ADD(R3, R3, R1); /* r3 := r3 + (~r2 + 1) OR r3 := r3 - r2 (len = end-start) */
RET();
/* readln: read a line until CR and fill in the TIB */
readln = LD(R1, tib); /* load TIB address */
LD(R0, toin); /* load >IN address */
STR(R1, R0, 0); /* make >IN point at the start of TIB */
readlp = TRAP(0x20); /* r0 = getchar() */
STR(R0, R1, 0); /* mem[r1] = r0 */
ADD(R1, R1, 1); /* r1 = r1 + 1 */
ADD(R0, R0, -10); /* is r0 == '\n' ? */
BRNP(readlp); /* no: read another character */
ADD(R1, R1, -1); /* r1 = r1 - 1 to erase newline */
STR(R0, R1, 0); /* write 0 instead */
BR(token); /* try to parse first token */
space = DW(-32);
toin = DW(TOIN);
tib = DW(TIB);
Unfortunately, we have to store the whitespace symbol (ASCII 32) in a separate memory cell because it’s too large to be an immediate value. Making it a negative integer saves us from subtraction instruction combo, so that we could use ADD instead. Now, if we call JSR(token) in a loop and print memory between R2 and R2+R3 after it - we would be getting word by word from the console. At this point we can start implementing the core of our post-apocalyptic Forth interpreter.
Dictionary
Before we start implementing the main interpreter loop, let’s agree on how Forth memory layout would look like.
Typically, a Forth VM uses two stacks - one for temporary variables (data stack), another for subroutine return addresses (return stack). We have the luxury of using dedicated registers as top stack pointers, but the start addresses of the stack must be predefined. We can use some arbitrary ranges, like 0x5000 for data and 0x6000 for return stack. We can also assign R5 to be the data stack pointer and R6 to be the return stack pointer. Let’s also make R4 an “instruction” pointer that would need a bit later. These three registers are sacred and no assembly code should use them beyond their primary purpose.
const int SPADDR = 0x5000; /* data stack address */
const int RPADDR = 0x6000; /* return stack address */
const int IP = R4; /* instruction pointer */
const int SP = R5; /* data stack pointer */
const int RP = R6; /* return stack pointer */
It’s now becoming clear how some of the Forth words could be implemented. For example @ would be taking a value from SP and fetching one cell of data at the address. ! would be fetching a value and address from SP and saving the value there. + would be fetching two values from SP and adding them and so on:
// @ (addr -- x)
LDR(R0, SP, 0);
LDR(R0, R0, 0);
STR(R0, SP, 0);
// ! (x addr --)
LDR(R0, SP, 0);
LDR(R1, SP, -1);
STR(R1, R0, 0);
ADD(SP, SP, -2);
// + (x y -- x+y)
LDR(R0, SP, 0);
LDR(R1, SP, -1);
ADD(R1, R1, R0);
ADD(SP, SP, -1);
STR(R1, SP, 0);
All these Forth words must be stored in a dictionary, so that Forth interpreter would be able to find them by their name and execute. It’s time to define the dictionary structure.
To keep things simple, a dictionary would be a linked list where each word contains a link to the previous word. Scanning a dictionary starts from the end of the list and goes to the head of it.
Besides, each word would be containing the word name and its name length, and some optional flags that might help with the execution of certain words (i.e. execute them immediately or compile them into the dictionary). Don’t bother too much with the flags, let’s just reserve a single byte for them and deal with it later. After the word header the body of the word comes, ending with a special BR(next) instruction that stops the execution of the current word and goes to the next one:
next = LDR(R0, IP, 0);
ADD(IP, IP, 1);
JMP(R0);
Since words are a linked list, we should store the address of the last word somewhere to simplify the creation of the new words. Typically a variable called “LATEST” is used for that.
We would need two more variables for a functional interpreter. One is to keep the interpreter state – interpreting words as they are typed, or compiling words into the new word definition. A variable STATE is used for that:
2 2 + \ <- these words are evaluated as they are entered,
\ immediately.
: four 2 2 + ; \ <- these words are appeneded to the "four" word
\ entry in the dictionary as they are entered.
The last variable would be HERE, storing a pointer to the latest appended (compiled) instruction of the latest word.
For convenience we can define a macro to define primitive words and variables. These words would be defined by the interpreter itself, in machine code, and would be stored at the beginning of the dictionary:
/* WORD creates a new word record without a body */
static void WORD(const char *name, int flags) {
int i;
link = DW(link); /* link to the previous word */
DW(strlen(name) + flags); /* length + flags */
for (i = 0; i < strlen(name); i++) {
DW(name[i]); /* word name */
}
}
/* VAR creates a new word that pushes the pointer to the data stack */
static void VAR(const char *name, int ptr, int next) {
WORD(name, 0);
LD(R0, ptr);
ADD(SP, SP, 1);
STR(R0, SP, 0);
BR(next);
}
...
/* @ ( addr -- x ) Fetch memory at addr */
WORD("@", 0);
LDR(R0, SP, 0);
LDR(R0, R0, 0);
STR(R0, SP, 0);
BR(next);
/* ! ( x addr -- ) Store x at addr */
WORD("!", 0);
LDR(R0, SP, 0);
LDR(R1, SP, -1);
STR(R1, R0, 0);
ADD(SP, SP, -2);
BR(next);
...
latest = DW(LATEST);
state = DW(STATE);
here = DW(HERE);
VAR("latest", latest, next);
VAR("state", state, next);
VAR("here", here, next);
Now if we scan the dictionary for word “state” and execute its body - it would put the value of the STATE variable onto stack. Similarly, if we scan the dictionary for the word “@” and execute it - it would allow us to fetch the value at given address. Implementing this lookup mechanism would give us a working interpreter and would successfully end our quest.
Interpreter
The interpreter starts with requesting a new token. Due to the scarcity of registers we should probably store new token pointer and its length somewhere. Data stack is a good choice, we wouldn’t need it during the interpreter lookup procedure anyway.
Then we should take the latest word, starting with the LATEST variable, and compare its length and its name to the token. If either length or any character in the name differs - we should continue our search. If the next word pointer becomes zero - we reached the end of the dictionary and the word is not found. This is a fatal error for our interpreter, at which we reset it brutally and start again. Apocalypse is not a time for typos in code.
Once the word is found – we should check the interpreter state. If it’s compiling – we should append the word start address to the current word definition. If it’s interpreting immediately - we should jump to the word body address and let it go from there.
It’s a rather long piece of code, but believe it or not, it contains the complete Forth interpreter for our VM.
/* read/eval main interpreter loop */
intrp = JSR(token); /* r1, r2 := (start, length) of the token in TIB */
STR(R2, SP, 2);
STR(R3, SP, 3);
LDI(R0, latest); /* r0 := [LATEST] */
ismtch = BRZ(error); /* if r0 == 0: goto error (word not found) */
STR(R0, SP, 1); /* push word code onto SP stack */
LDR(R1, SP, 2);
LDR(R2, SP, 3);
LDR(R3, R0, 1); /* r3 := [link+1] (word length) */
AND(R3, R3, 0xf); /* r3 := word length */
NOT(R3, R3);
ADD(R3, R3, 1);
ADD(R3, R3, R2); /* r3 := r3 - r2 (compare length) */
BRNP(nomtch); /* if length differs - try next word */
nextc = LDR(IP, R0, 2); /* ip := [r0+2] (nth word letter from dict) */
LDR(R3, R1, 0); /* r2 := [r1] (nth word letter from token) */
NOT(R3, R3);
ADD(R3, R3, 1);
ADD(R3, R3, IP); /* compare ip and r2 */
BRNP(nomtch); /* if letters don't match - try next word */
ADD(R1, R1, 1); /* advance letter counter for token */
ADD(R0, R0, 1); /* advance letter counter for dict */
ADD(R2, R2, -1); /* decrease remaining length */
BRZ(found); /* if remaining length == 0: found a word! */
BR(nextc);
nomtch = LDR(R0, SP, 1); /* restore link */
LDR(R0, R0, 0); /* r0 := [r0] (next link) */
BR(ismtch);
found = ADD(R0, R0, 2);
LEA(IP, loop);
LDI(R1, state);
LDR(R2, SP, 1); /* restore word code from SP */
LDR(R2, R2, 1); /* get word length and flags */
AND(R2, R2, 0x10);
ADD(R2, R2, R1);
ADD(R2, R2, -1);
BRZ(compil);
JMP(R0);
loop = DW(intrp);
What’s missing here is the “compile” part, which does nothing more but storing R0 into HERE and advancing the HERE address:
compil = LDI(R1, here);
STR(R0, R1, 0); /* here := r0 */
ADD(R1, R1, 1);
STI(R1, here); /* here := here + 1 */
BR(next);
Actually, if we launch our interpreter at this point, define some primitive words like “1”, “2” or “+” and ask it to evaluate “1 2 +” – it would be able to find and interpret all the words correctly, leaving 3 at the top of the data stack.
But we need to support user-defined words, too. User words usually start with : word and end with ;. So all we need to do is to define primitives for : and ;.
Let’s start with ;. This is the only immediate word in our dictionary and the reason we had the flags byte. When this word is found and the interpreter is in the compilation state - it evaluates the word ; immediately anyway, instead of compiling it.
What ; does is switching the interpreter to the regular state (interpreting) and appends “exit” word to the end of the current word definition, which would pop the address from the return stack and jump to it:
WORD(";", F_IMMEDIATE);
AND(R1, R1, 0);
STI(R1, state); /* state := 0 */
LEA(R0, exit); /* compile "exit" */
BRZ(compil);
WORD("exit", 0);
exit = LDR(IP, RP, 0);
ADD(RP, RP, -1);
BR(next);
If you recall, in the interpreter loop before jumping to the word execution we stored the interpreter loop address into IP so that at the end of the word we would fall back to the interpreter.
Now, all that’s left is : word, allowing us to extend the dictionary with custom, user-defined words, like : four 2 2 + ;. What : does can be seen as two operations. First, it reads the next token and creates a new record in the dictionary. Then it compiles down the special docol word and switches the VM to the “compiling” state. All further tokens (words) get compiled into the current word definition until ; is found, terminating the word.
Why is this docol so special and why is it needed at all?
Subroutine threading:
┌─────────┐
┌────►│DUP:.... │
┌─────────┐ │ │ RET │
│ DUP ├──►call DUP ├─────────┤
├─────────┤ call PLUS ─►│PLUS: ...│
│ PLUS │ call PRINT │ RET │
├─────────┤ │ ├─────────┤
│ PRINT │ └───►│PRINT: ..│
└─────────┘ │ RET │
└─────────┘
Direct threading:
┌──────────────────────────────┐
│ │
│ ┌─────────┐ ┌───────┴───┐
│ ┌────►│DUP:.... │ │next: │
┌─────────┐ ▼ │ │ JMP next├──► JMP(IP++)│
│ DUP ├──► jmp DUP ├─────────┤ └───▲───▲───┘
├─────────┤ jmp PLUS ─►│PLUS: ...│ │ │
│ PLUS │ jmp PRINT │ JMP next├──────┘ │
├─────────┤ │ ├─────────┤ │
│ PRINT │ └───►│PRINT: ..│ │
└─────────┘ │ JMP next├──────────┘
└─────────┘
There’s a slight difference in these two illustrations.
If we were using subroutine threading - our words would be represented as a sequence of “call” instructions. Each “call” would put the IP on return stack, and restore it when the related subroutine exited, going to the next “call”. But we use direct threading here, and it’s next that increases the IP. So if suddenly while executing one word we want to call another, non-primitive, word - we should store the return address manually. What docol does is just this: push IP and jump to the next sub-word in the current word definition.
WORD(":", 0);
JSR(token); /* read next token after colon */
LDI(R0, latest);
LDI(R1, here);
STR(R0, R1, 0); /* [HERE] := LATEST (write link) */
STI(R1, latest); /* LATEST := HERE (update latest pointer) */
STR(R3, R1, 1); /* write word length at [HERE+1] */
ADD(R1, R1, 2); /* advance here by 2 cells */
copy = LDR(R0, R2, 0); /* copy from R2..(R2+R3) to HERE */
STR(R0, R1, 0);
ADD(R2, R2, 1);
ADD(R1, R1, 1);
ADD(R3, R3, -1);
BRP(copy);
LD(R0, op1); /* store absolute jump to "docol" (see opcodes below) */
STR(R0, R1, 0); /* ... */
LD(R0, op2); /* ... */
STR(R0, R1, 1); /* ... */
LD(R0, op3); /* ... */
STR(R0, R1, 2); /* ... */
ADD(R1, R1, 3); /* advance HERE over those 3 instructions */
STI(R1, here); /* update HERE := R1 */
AND(R2, R2, 0); /* r2 := 0 */
ADD(R2, R2, 1); /* r2 := r2 + 1 */
STI(R2, state); /* state := 1 ("compiling") */
BR(next);
op1 = DW(0x2201); /* LD(R1, PC+1) */
op2 = DW(0xc040); /* JMP(R1) */
op3 = DW(docol); /* FILL [docol] */
docol = STR(IP, RP, 1); /* store current IP on return stack */
ADD(RP, RP, 1);
ADD(IP, R0, 3); /* skip compiled LD+JMP+FILL and advance IP */
BR(next);
There is a quirky part with op1, op2 and op3. Once the new word header is created, LATEST and HERE are both updated - we must compile some machine code that would jump to docol label. Since LC-3 has no support for absolute jumps, it could be either a relative or an indirect jump. Calculating relative addresses would be a nightmare, but an indirect jump is rather straightforward: store label address at some place, use LD to load it and perform a JMP. These three instructions are compiled literally into every non-primitive word definition:
┌────────┐
│: twice │
┌─────┐ ├────────┤
IP=10│5 │ ┌─►│ docol │ IP=50
├─────┤ │ ├────────┤
IP=11│twice├─┘ │ dup │ IP=51
├─────┤ ├────────┤
IP=12│. │◄┐ │ + │ IP=52
└─────┘ │ ├────────┤
└──┤ ; │ IP=53
└────────┘
Here’s an example of executing 5 twice . which starts at IP=10 address. When it’s time to call twice the IP is incremented from 11 to 12 and next jumps to the first cell in twice word definition. That would be docol at address 50. It pushes IP=12 to RP stack, sets IP to 50 and calls next. This continues to dup, then next, then +, then next, then ;, which restores the IP from the RP stack, setting it to 12 and jumping to it. This is how the interpreter returns back to the following . word.
With some luck we should be able to define the following primitive words in assembly:
WORDS:
@ ( addr -- x ) \ Fetch memory at addr
! ( x addr -- ) \ Store x at addr
sp@ ( -- addr ) \ Get current data pointer
rp@ ( -- addr ) \ Get current stack pointer
=0 ( x -- f ) \ if *sp == 0 then -1 else 0
+ ( a b -- a+b ) \ add two values on top of the data stack
nand ( a b -- n ) \ a NAND b
key ( -- k ) \ Read a key from console
emit ( c -- ) \ Write a character to console
bye ( -- ) \ Terminate the VM
VARIABLES:
tib \ TIB address (last line of input)
>in \ read pointer to TIB
latest \ latest word address
state \ interpreter state
here \ last compiled word address
If you are curious - please check out the repo to see how they are implemented.
Extending our Forth
At this point, our interpreter can evaluate primitive words and allows defining custom, compound words. But how useful is that if we don’t even have numbers?!
Let’s define our first word, the most useful one:
\ Fetch value from the top of the data stack, effectively duplicating it
: dup sp@ @ ;
Now we can define some numbers!
: -1 dup dup nand dup dup nand nand ;
: 0 -1 dup nand ;
: 1 -1 dup + dup nand ;
: 2 1 1 + ;
: 3 2 1 + ;
: 4 2 2 + ;
...
: 16 8 8 + ;
Here only -1 is a tricky one. For any value n on stack that would calculate:
: -1 \ n
dup \ n n
dup \ n n n
nand \ n !n (n NAND n = NOT n)
dup \ n !n !n
dup \ n !n !n !n
nand \ n !n n (!n NAND !n = n)
nand \ n !0 (n AND !n = 0, n NAND !n = !0 = -1)
;
This would work with an empty stack as well, since it does not modify the topmost stack value so if there’s some garbage stored in RAM at (sp-1) address - it would leave that and put -1 over it. The rest of the number literals can be added ad infinitum using nand or +.
We can also introduce some arithmetic helpers:
: invert dup nand ;
: and nand invert ;
: negate invert 1 + ;
: - negate + ;
: = - 0= ;
: <> = invert ;
Time to add some typical Forth stack operations, since we now have arithmetics and a stack pointer variable:
: drop dup - + ;
: over sp@ 1 - @ ;
: swap over over sp@ 3 - ! sp@ 1 - ! ;
: nip swap drop ;
: 2dup over over ;
: 2drop drop drop ;
Easy so far? Let’s spice it up. So far our numbers were “calculated” at runtime, so every time we need a 16 - we perform lots of nands and dups only to get that number. Can we speed it up? Yes, we may introduce an “immediate” mode, where some Forth code is evaluated as it is entered and the result of it gets compiled into a word, say:
\ slow
: four 1 1 1 1 + + + ;
\ fast
: four lit [ 1 1 1 1 + + + , ] ;
Here [ and ] outline the “immediate” mode, which evaluates the code as it gets entered (even if the word around is compiled). Comma is used to advance HERE pointer and lit uses the following cell as the literal to put on data stack, i.e. if the word definition contains lit followed by a cell with value 0x0004 - lit would put 0x0004 on stack and jump over it to the next instruction. Now, how do we implement these?
\ compile value to HERE, advance HERE
: , here @ ! here @ 1 + here ! ;
\ mark last word as F_IMMEDIATE
: immediate latest @ 1 + dup @ 16 or swap ! ;
\ enter "interpret" mode, immediately
: [ 0 state ! ; immediate
\ leave "interpret" mode and keep compiling
: ] 1 state ! ;
\ put next compiled value onto data stack
: lit rp@ @ dup 1 + rp@ ! @ ;
With a few low-level pointer manipulations we can add core words to manage the return stack:
: >rexit rp@ ! ;
: >r rp@ @ swap rp@ ! >rexit ;
: r> rp@ 1 - @ rp@ @ rp@ 1 - ! lit [ here @ 3 + , ] rp@ ! ;
This may look confusing at a first glance, because pushing data to the return stack does not seem to advance the rp@ pointer. But look closer how >rexit works: it overwrites the return address with the value from the data stack and returns to that address. The semicolon in >r is never executed!
Let’s try a simple example adding a few imaginative breakpoints to see how data and return stacks would look like. Breakpoints are notated in curly braces.
: >rexit {G} rp@ ! {H} ;
: >r {C} rp@ @ {D} swap {E} rp@ ! {F} >rexit ;
3 {A} >r {B}
DATA | RET
A: 3 | | About to enter >r
C: 3 | A | Inside >r, A is return address
D: 3 A | A | Fetched rp@ to data stack
E: A 3 | A | Swapped values on data stack
F: A | 3 | Stored top data value at return stack pointer
G: A | 3 F | Entered >rexit, F is return address
H: | 3 A | Replaced return address with a value from data stack
B: | 3 | And naturally returned to A+1, done!
Now we can implement plenty of other words, such as “rot”, branches, if/then/else, various loops. With some luck we can introduce variables and create word to define new words from within Forth. We can add a custom input parser, at least to support strings, but maybe a better input editor could also be created, to support arrow keys, line editing etc.
Finally, a code like this can be interactively entered into our Forth machine:
: four 2 2 + ;
four four 1 + .s
." done" cr
\ Output:
\ <2> 4 5
\ done
Here we defined a custom word at runtime, put some values on data stack and called a debug routine (also written in Forth) to dump the contents of the data stack, printed some strings - that feels like a real programming language now!
Summary
This is nothing but a little experiment to bootstrap a Forth system on a tiny limited CPU.
You may find the complete source code of the VM, the interpreter and the Forth “core library” at github.com/zserge/lc3-forth
It takes 287 machine words, or 574 bytes. This could theoretically be designed on paper and entered by hand on some hexpad to program the first computer.
But sure, programming after the apocalypse is no fun, and this sort of bare metal engineering isn’t easy at all. Perhaps, this article could serve as an additional motivation to avoid the end of the world for as long as we can.
I hope you’ve enjoyed this article. You can follow – and contribute to – on Github, Mastodon, Twitter or subscribe via rss.
Aug 04, 2022
See also: Learn a language by writing too many Forths and more.